Bayesian HMM-GLMs

Prediction of the propensity to donate in the blood donors in Trieste

Erik De Luca

erik.deluca@studenti.units.it

Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche

Tommaso Piscitelli

tommaso.piscitelli@studenti.units.it

Dipartimento di Informatica, Matematica e Geoscienze

Summary

About the data
Bayesian HMM with GLM on emissions
Viterbi algorithm
Check of the model
Number of latent states

About the Data

What we have

A longitudinal panel of 9,000+ unique blood donors in Trieste
Annual counts of donations per donor (0–4 per year), spanning 2009–2023

Where it comes from

ASUGI transfusion service operational registers
Fully anonymised data; available covariates: gender (M/F) and year of birth

Objective

Build a predictive model for future donation propensity and counts
Discover latent behavioural profiles and common temporal patterns
Quantify the impact of age, gender, and shocks (e.g., COVID-19) on dynamics

Limitations

Sparse covariates (only gender and birth year)
No clinical or socio-economic info

Bayesian HMM with GLM on emissions

Initial-state distribution (\(\pi\)):

\(\pi_{\text{base}}\sim\mathrm{Dirichlet}(\boldsymbol{\alpha}_{\pi})\)
\[ \Pr(z_{n,0}=k\mid x^{\pi}_n)= \operatorname{softmax}_k\!\bigl( \log\pi_{\text{base},k}+W_{\pi,k}\cdot x^{\pi}_n \bigr) \]
\(x^{\pi}_n = (\text{intercept}, \text{birth_year_norm},\;\text{gender_code})\in\mathbb R^{3}\)

Transition dynamics (\(A\))

\(A_{\text{base}}[k,\cdot]\sim\mathrm{Dirichlet}(\boldsymbol{\alpha}_{A_k})\)
\[ \Pr(z_{n,t}=j\mid z_{n,t-1}=k,\;x^{A}_{n,t})= \operatorname{softmax}_j\!\bigl( \log A_{\text{base},kj}+W_{A,kj}\cdot x^{A}_{n,t} \bigr). \]
\(x^{A}_{n,t} = (\text{intercept}, \text{age_binned}, \text{covid_years})\in\mathbb R^{8}\)

Emission (\(\lambda\)):

\[ y_{n,t} \mid z_{n,t}=k \sim \mathrm{Poisson}\Big( \exp\Big(\beta_{em,k} \cdot x^{em}_{n,t} \Big) \Big) \]
\(x^{em}_{n,t} = (\text{intercept}, \text{gender}, \text{age_binned},\;\text{covid_years})\in\mathbb R^{9}\)

Results

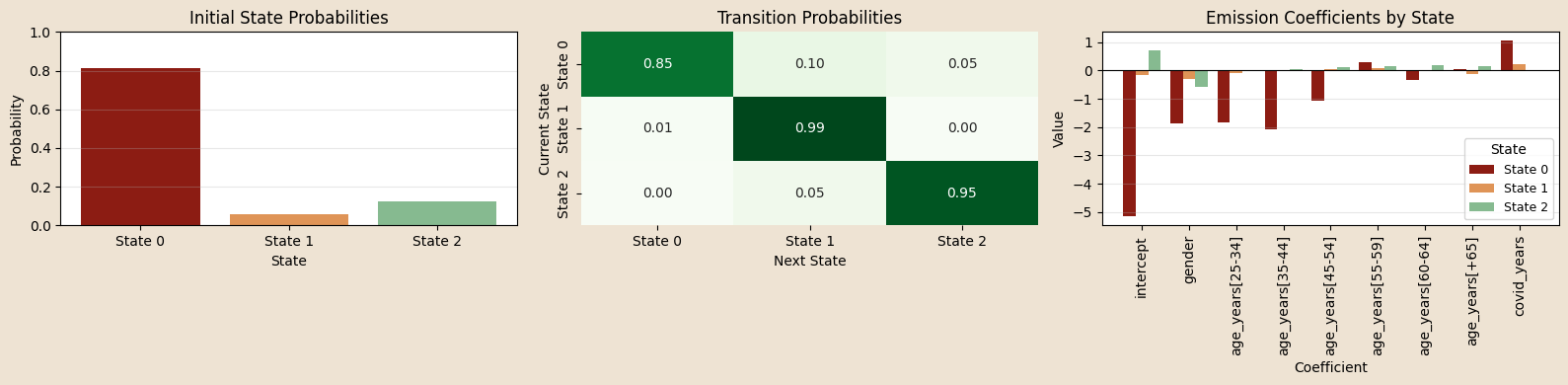
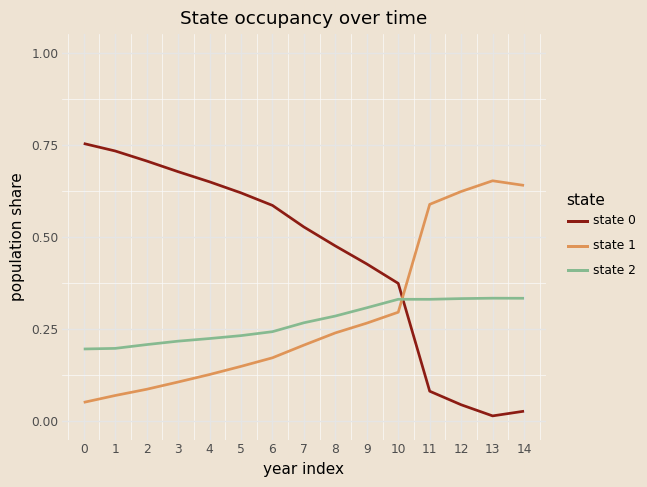
Coefficients on \(\pi\)

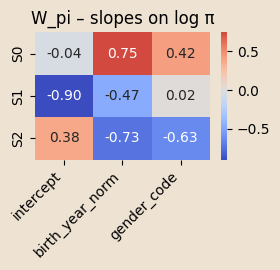
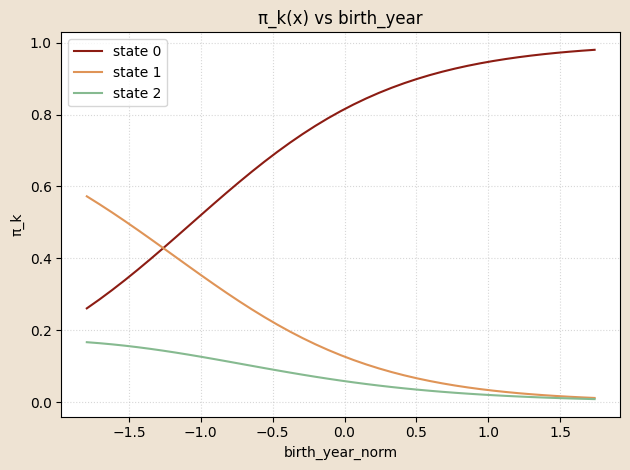
Coefficients on \(A\)

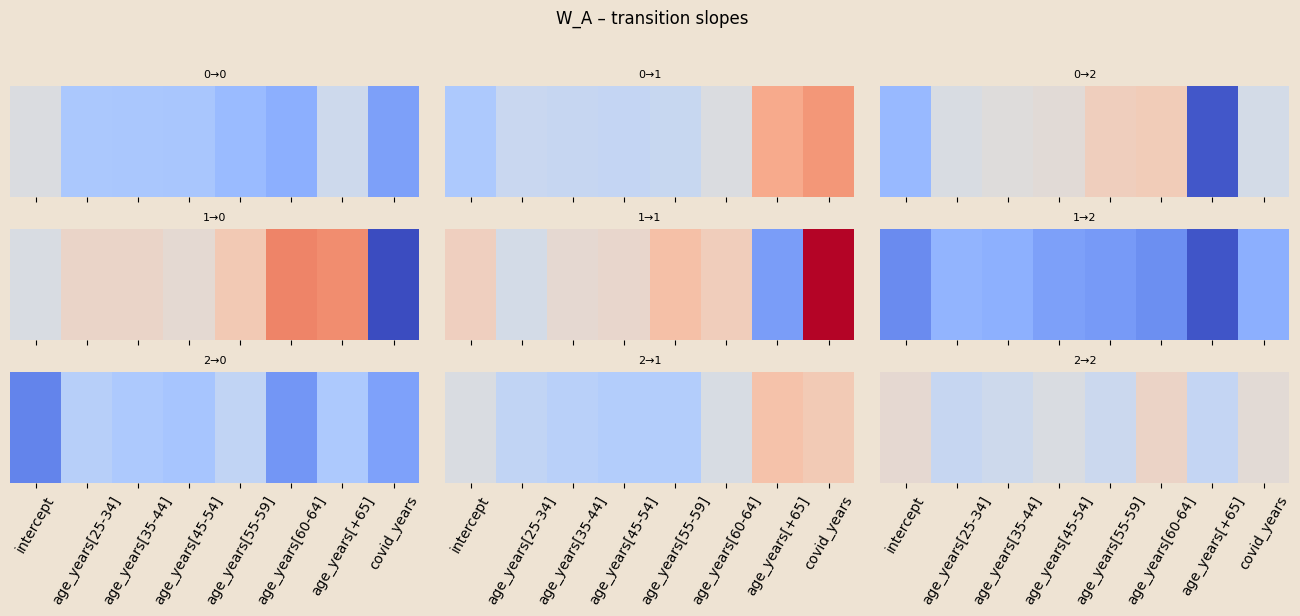
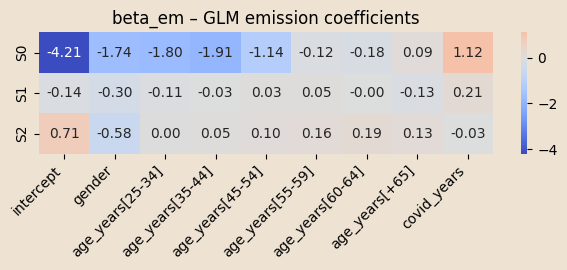
\(\beta\) coefficients

Viterbi Algorithm

Goal: for each donor find the MAP latent path \(z_{0:T}^\ast\).
Dynamic programming
- Initial step
  \[ \delta_0(k)=\log\hat\pi_k+\log\text{Poisson}(y_0\mid\hat\lambda_k) \]
- Recursion for \(t=1,\dots,T\)
  \[ \delta_t(j)=\max_k\bigl[\delta_{t-1}(k)+\log\hat A_{k j}\bigr] +\log\text{Poisson}(y_t\mid\hat\lambda_j), \] \[ \psi_t(j)=\arg\max_k\bigl[\delta_{t-1}(k)+\log\hat A_{k j}\bigr] \]
- Back-tracking
  
  Start with \(z_T^\ast=\arg\max_k\delta_T(k)\), then \(z_{t-1}^\ast=\psi_t(z_t^\ast)\) for \(t=T,\dots,1\).

Examples

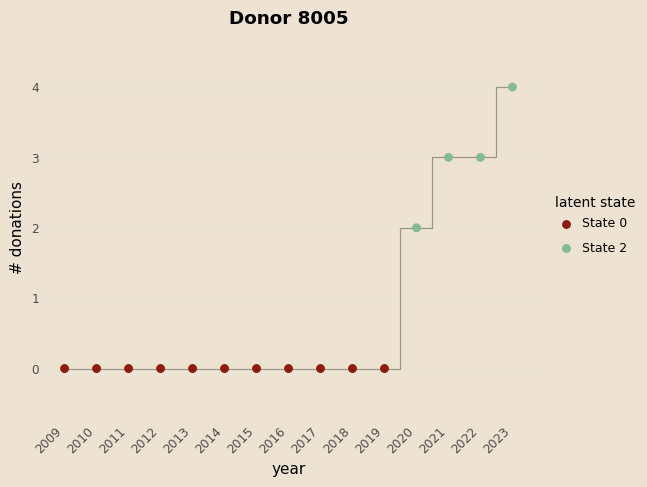
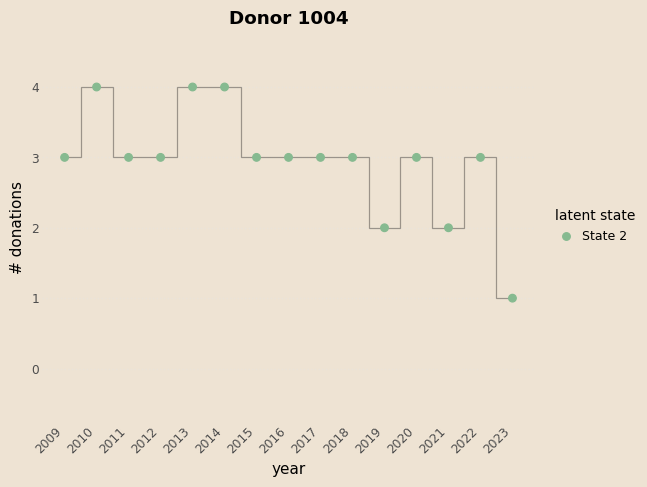
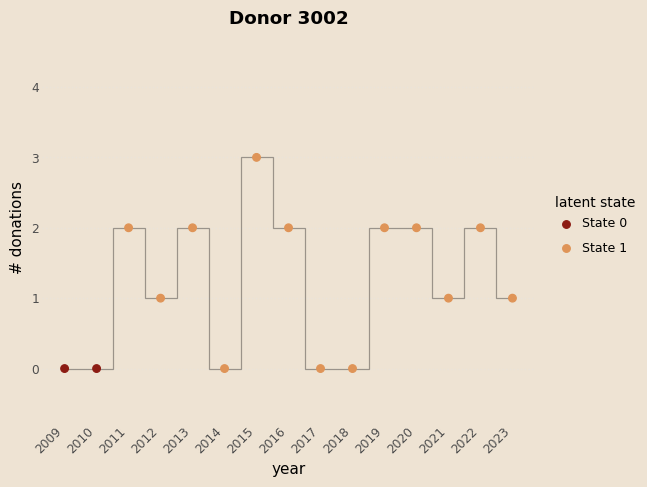
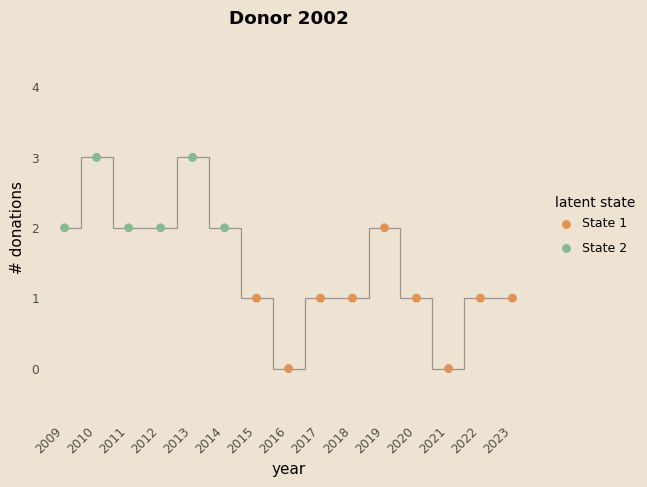
Prediction

# Forward filtering to get alpha_T for prediction
log_alpha = torch.empty(1, T_hist, K, dtype=torch.float32)
log_alpha[:, 0] = log_pi + emis_log[:, 0]

for t in range(1, T_hist):
    x_t = xA_te[:, t, :]
    logits = logA0.unsqueeze(0) + (W_A_t.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)  # (1,K,K)
    log_A  = logits - torch.logsumexp(logits, dim=2, keepdim=True)
    log_alpha[:, t] = torch.logsumexp(log_alpha[:, t - 1].unsqueeze(2) + log_A, dim=1) + emis_log[:, t]

alpha_T = (log_alpha[:, -1] - torch.logsumexp(log_alpha[:, -1], dim=1, keepdim=True)).exp().cpu().numpy()[0]  # (K,)

# Next-year transition and emission
logits_next = np.log(A_base + 1e-30) + np.tensordot(W_A, x_A_next, axes=([2], [0]))  # (K,K)
A_next = _softmax_np(logits_next)                                                     # (K,K)
p_next = alpha_T @ A_next                                                             # (K,)

lam_next = np.exp(beta_em[:, 0] + (beta_em[:, 1:] @ x_em_next))                       # (K,)

# Predictive mixture for next year
expected_next = float((p_next * lam_next).sum())
p0 = float((p_next * np.exp(-lam_next)).sum())
prob_donate_next = 1.0 - p0

from scipy.stats import poisson as _po
pmf0k = np.array([(p_next * _po.pmf(k, lam_next)).sum() for k in range(max_k + 1)], dtype=float)
tail  = float(max(0.0, 1.0 - pmf0k.sum()))
pmf_dict = {str(k): float(pmf0k[k]) for k in range(max_k + 1)}
pmf_dict[f">={max_k+1}"] = tail

foward algoritm \[ \left\{ \begin{aligned} & \alpha(z_0) = P(x_0 \mid z_0)\, P(z_0) \\ & \alpha(z_T) = P(x_T \mid z_T)\, \sum_{z_{T-1}} P(z_{T} \mid z_{T-1}) \,\alpha(z_{T-1}) \end{aligned} \right. \]

Prediction

# Forward filtering to get alpha_T for prediction
log_alpha = torch.empty(1, T_hist, K, dtype=torch.float32)
log_alpha[:, 0] = log_pi + emis_log[:, 0]

for t in range(1, T_hist):
    x_t = xA_te[:, t, :]
    logits = logA0.unsqueeze(0) + (W_A_t.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)  # (1,K,K)
    log_A  = logits - torch.logsumexp(logits, dim=2, keepdim=True)
    log_alpha[:, t] = torch.logsumexp(log_alpha[:, t - 1].unsqueeze(2) + log_A, dim=1) + emis_log[:, t]

alpha_T = (log_alpha[:, -1] - torch.logsumexp(log_alpha[:, -1], dim=1, keepdim=True)).exp().cpu().numpy()[0]  # (K,)

# Next-year transition and emission
logits_next = np.log(A_base + 1e-30) + np.tensordot(W_A, x_A_next, axes=([2], [0]))  # (K,K)
A_next = _softmax_np(logits_next)                                                     # (K,K)
p_next = alpha_T @ A_next                                                             # (K,)

lam_next = np.exp(beta_em[:, 0] + (beta_em[:, 1:] @ x_em_next))                       # (K,)

# Predictive mixture for next year
expected_next = float((p_next * lam_next).sum())
p0 = float((p_next * np.exp(-lam_next)).sum())
prob_donate_next = 1.0 - p0

from scipy.stats import poisson as _po
pmf0k = np.array([(p_next * _po.pmf(k, lam_next)).sum() for k in range(max_k + 1)], dtype=float)
tail  = float(max(0.0, 1.0 - pmf0k.sum()))
pmf_dict = {str(k): float(pmf0k[k]) for k in range(max_k + 1)}
pmf_dict[f">={max_k+1}"] = tail

Predictive state ditribution \[ P(z_{T+1}) = \alpha(z_T) \times A_{next}(x^{next}_A) \]

Prediction

# Forward filtering to get alpha_T for prediction
log_alpha = torch.empty(1, T_hist, K, dtype=torch.float32)
log_alpha[:, 0] = log_pi + emis_log[:, 0]

for t in range(1, T_hist):
    x_t = xA_te[:, t, :]
    logits = logA0.unsqueeze(0) + (W_A_t.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)  # (1,K,K)
    log_A  = logits - torch.logsumexp(logits, dim=2, keepdim=True)
    log_alpha[:, t] = torch.logsumexp(log_alpha[:, t - 1].unsqueeze(2) + log_A, dim=1) + emis_log[:, t]

alpha_T = (log_alpha[:, -1] - torch.logsumexp(log_alpha[:, -1], dim=1, keepdim=True)).exp().cpu().numpy()[0]  # (K,)

# Next-year transition and emission
logits_next = np.log(A_base + 1e-30) + np.tensordot(W_A, x_A_next, axes=([2], [0]))  # (K,K)
A_next = _softmax_np(logits_next)                                                     # (K,K)
p_next = alpha_T @ A_next                                                             # (K,)

lam_next = np.exp((beta_em[:,:] @ x_em_next))                       # (K,)

# Predictive mixture for next year
expected_next = float((p_next * lam_next).sum())
p0 = float((p_next * np.exp(-lam_next)).sum())
prob_donate_next = 1.0 - p0

from scipy.stats import poisson as _po
pmf0k = np.array([(p_next * _po.pmf(k, lam_next)).sum() for k in range(max_k + 1)], dtype=float)
tail  = float(max(0.0, 1.0 - pmf0k.sum()))
pmf_dict = {str(k): float(pmf0k[k]) for k in range(max_k + 1)}
pmf_dict[f">={max_k+1}"] = tail

Predictive number of donation (Mixture of Poisson) \[ \mathbb{E}[y_{T+1}] = \sum_{k=1}^K p_{T+1}(k)\,\lambda_{T+1}(k) \] \[ \Pr(y_{T+1} = k) = \sum_{i=1}^K p_{T+1}(i)\,\text{Poisson}\!\bigl(k \mid \lambda_{T+1}(i)\bigr) \]

Example

Years	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021	2022
Counts	0	0	0	3	4	3	4	3	4	3	2	2	2	3
Viterbi st.	0	0	0	2	2	2	2	2	2	2	2	2	2	2

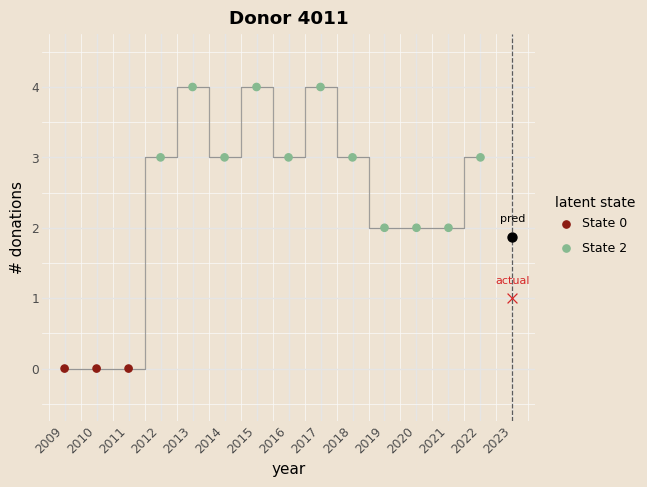
Next-state probabilities: [0.005, 0.125, 0.870]

Expected next donations: 1.871

Prob donate next: 0.824

# donations	0	1	2	3	4	>=5
Probability	0.175	0.275	0.252	0.164	0.082	0.049

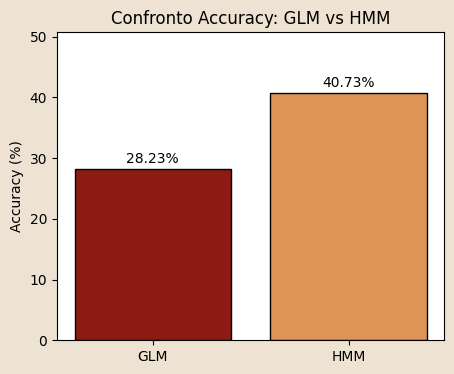
Evaluate performance

Compare the model with a GLM

\[ y_{n,t} \mid z_{n,t}=k \sim \mathrm{Poisson}\Big( \exp\Big(\beta_{em,k} \cdot x^{em}_{n,t} \Big) \Big) \]

\[ x^{em}_{n,t} = (\text{intercept}, \text{gender}, \text{age_binned},\;\text{covid_years})\in\mathbb R^{9} \]

Metric	GLM	HMM	Abs diff	Rel diff %
pred mean	0.96	0.41	0.55	135.46%
obs mean	0.91	0.91	0.00	0.00%
MSE	1.0158	1.2934	-0.2777	-21.47%
Accuracy (round)	28.23%	40.73%	-12.50pp	-30.69%

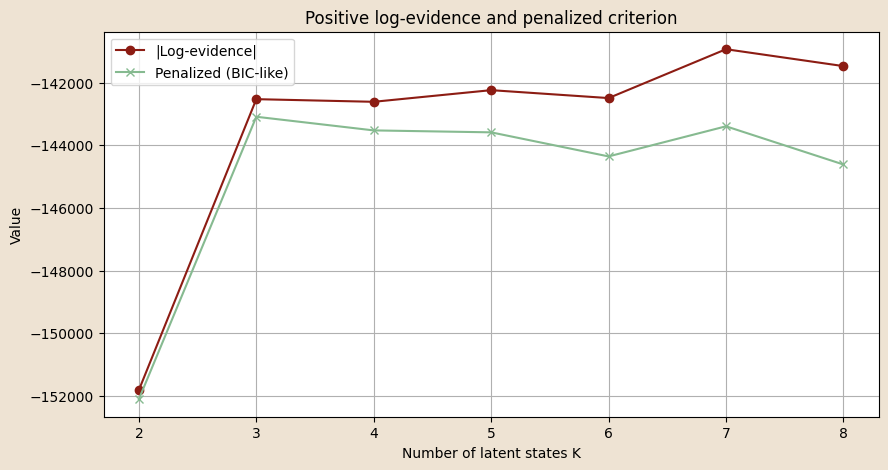
Number of Latent States

Goal: estimate model evidence (Laplace approximation) for differnt values of number of states

\[ \log p(X) \;\approx\; \log p\!\left(X \mid \hat{\theta}_{\text{MAP}}\right) \;+\; \text{Occam factor} \]

\[ \text{Occam factor} \;\approx\; -\tfrac{1}{2} M \, \ln N \]

Forward algorithm per valutare la likeliood function corrispondente ai parametri appresi

\[ \left\{ \begin{aligned} & \alpha(z_0) \;=\; p(z_0)\, p(x_0 \mid z_0) \\ & \alpha(z_T) \;=\; p(x_T \mid z_T)\; \sum_{z_{n-1}} \alpha(z_{n-1})\, p(z_n \mid z_{n-1}) \quad\text{per } n = 1,\dots, T. \end{aligned} \right. \; ; \quad \sum_{z_{T}} \alpha(z_{T}) = p\!\left(X \mid \hat{\theta}_{\text{MAP}}\right) \]

Conclusions

The Bayesian HMM-GLMs permit to get the dynamic and hidden behavioural of the donors
The model is an easy to read and to communicate but at the same time flexible
The latent states are well defined and show a clear donation pattern

Thanks

Backup

Model in Pyro

@config_enumerate
def model(obs, x_pi, x_A, x_em):
    N, T = obs.shape

    # 1) Priors/parameters for initial and transition distribution
    pi_base = pyro.sample("pi_base", dist.Dirichlet(alpha_pi))          # [K]
    A_base  = pyro.sample("A_base",  dist.Dirichlet(alpha_A).to_event(1)) # [K, K]
    log_pi_base = pi_base.log()
    log_A_base  = A_base.log()

    # 2) Slope coefficients for initial and transition covariates (learned)
    W_pi = pyro.param("W_pi", torch.zeros(K, C_pi))                  # [K, C_pi]
    W_A  = pyro.param("W_A", torch.zeros(K, K, C_A))                 # [K, K, C_A]

    # 3) State-specific GLM emission coefficients (learned)
    beta_em = pyro.param("beta_em", torch.zeros(K, C_em))        # [K, C_em+1] (intercept + 9 dummies)

    with pyro.plate("seqs", N):
        # Initial hidden state probabilities: depend on x_pi via W_pi
        logits0 = log_pi_base + (x_pi @ W_pi.T)                      # [N, K]
        z_prev = pyro.sample("z_0",
                             dist.Categorical(logits=logits0),
                             infer={"enumerate": "parallel"})

        # Emission at t=0: state-specific GLM on covariates x_em[:, 0, :]
        log_mu0 = (x_em[:, 0, :] * beta_em[z_prev, :]).sum(-1)
        pyro.sample("y_0", dist.Poisson(log_mu0.exp()), obs=obs[:, 0])

        # For t = 1 ... T-1, update state and emit
        for t in range(1, T):
            x_t = x_A[:, t, :]                                      # [N, C_A]
            logitsT = (log_A_base[z_prev] + (W_A[z_prev] * x_t[:, None, :]).sum(-1))     # [N, K]
            z_t = pyro.sample(f"z_{t}",
                             dist.Categorical(logits=logitsT),
                             infer={"enumerate": "parallel"})

            # Emission: state-specific GLM at time t
            log_mu_t = (x_em[:, t, :] * beta_em[z_t, :]).sum(-1)
            pyro.sample(f"y_{t}", dist.Poisson(log_mu_t.exp()), obs=obs[:, t])
            z_prev = z_t

GLM on emissions

Priors: the same of the Bayesian HMM.

Slope parameters to learn

\(W_\pi \in \mathbb{R}^{K\times 2}\) (birth_year_norm, gender_code)
\(W_A \in \mathbb{R}^{K\times K \times 8}\) (seven age-bin dummies ages_norm, covid_years)
\(\beta_{em} \in \mathbb{R}^{K \times (1+9)}\) (intercept, gender_code_tile, ages_norm, covid_years)

Initial-state distribution

\[ \Pr(z_{n,0}=k \mid x^\pi_n) = \mathrm{softmax}_k \big( \log \pi_{\text{base},k} + W_{\pi,k} \cdot x^\pi_n \big) \]

Transition distribution

\[ \Pr(z_{n,t}=j \mid z_{n,t-1}=k, \ x^A_{n,t}) = \mathrm{softmax}_j \big( \log A_{\text{base},kj} + W_{A,kj} \cdot x^A_{n,t} \big) \]

Emission (one Poisson GLM for each latent state)

\[ y_{n,t} \mid z_{n,t}=k \sim \mathrm{Poisson}\Big( \exp\Big( \beta_{em,k,0} + \sum_{m=1}^{9} \beta_{em,k,m} \cdot x^{em}_{n,t,m} \Big) \Big) \]

Guide

Point-mass approximation:

\(q(\pi_{\text{base}})=\delta(\pi_{\text{base}}-\hat\pi)\),
\(q(A_{\text{base}})=\delta(A_{\text{base}}-\hat A)\).

All \(\lambda\), \(W_\pi\), \(W_A\) are deterministic pyro.params and they are optimized during the training. Discrete states \(z_{n,t}\) are enumerated exactly, allowing all possible configurations to be calculated using TraceEnum_ELBO (without stochastic approximation).

def guide(obs, x_pi, x_A, x_em):
    pi_q = pyro.param(
        "pi_base_map",
        torch.tensor([0.6, 0.3, 0.1]),
        constraint=dist.constraints.simplex
    )

    # Each row: simplex for state-to-state transitions
    A_init = torch.eye(K) * (K - 1.) + 1.
    A_init = A_init / A_init.sum(-1, keepdim=True)
    A_q = pyro.param(
        "A_base_map",
        A_init,
        constraint=dist.constraints.simplex
    )

    pyro.sample("pi_base", dist.Delta(pi_q).to_event(1))
    pyro.sample("A_base",  dist.Delta(A_q).to_event(2))

Train and Test

Split	Mean LL/seq	MAE	RMSE	Brier(y>0)	NLL
Test	-13.052	0.5068	0.7679	0.1797	0.8832
Train	-13.469	0.5183	0.7834	0.1790	0.9158

Viterbi Algorithm

@torch.no_grad()
def viterbi_paths_glm(obs, x_pi, x_A, x_em, model_path=None):
    """
    Viterbi decoding for HMM with covariate-dependent pi, A, 
    and Poisson-GLM emissions (intercept already included in covariates).

    Parameters
    ----------
    obs  : (N, T) long
        Observed counts.
    x_pi : (N, C_pi) float
        Covariates for initial state distribution.
    x_A  : (N, T, C_A) float
        Covariates for transition probabilities.
    x_em : (N, T, C_em) float
        Covariates for emission GLM (already includes intercept).
    model_path : str or Path, optional
        Path to saved HMM parameters.

    Returns
    -------
    paths : (N, T) long tensor on CPU
        Most likely latent state sequence for each sequence.
    """
    # ---------------- load parameters ----------------
    W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(model_path)

    # ---------------- device alignment ----------------
    device = obs.device
    obs = obs.to(device=device)
    x_pi = x_pi.to(device=device, dtype=torch.float32)
    x_A = x_A.to(device=device, dtype=torch.float32)
    x_em = x_em.to(device=device, dtype=torch.float32)

    W_pi   = _coerce_to_torch(W_pi, device)
    W_A    = _coerce_to_torch(W_A, device)
    pi_base = _coerce_to_torch(pi_base, device)
    A_base  = _coerce_to_torch(A_base, device)
    beta_em = _coerce_to_torch(beta_em, device)

    N, T = obs.shape
    K = int(pi_base.shape[0])

    # ---------------- emission log-probs ----------------
    # eta[n,t,k] = x_em[n,t,:] @ beta_em[k,:]
    eta = torch.einsum("ntc,kc->ntk", x_em, beta_em)  # (N,T,K)
    emis_log = dist.Poisson(rate=eta.exp()).log_prob(obs.unsqueeze(-1))  # (N,T,K)

    # ---------------- initial distribution ----------------
    log_pi_base = torch.log(pi_base + 1e-30)                 # (K,)
    logits0 = log_pi_base.view(1, K) + x_pi @ W_pi.T         # (N,K)
    log_pi = log_softmax_logits(logits0, dim=1)              # (N,K)

    delta = log_pi + emis_log[:, 0]                          # (N,K)
    psi = torch.zeros(N, T, K, dtype=torch.long, device=device)

    # ---------------- forward DP ----------------
    log_A_base = torch.log(A_base + 1e-30)                   # (K,K)
    for t in range(1, T):
        x_t = x_A[:, t, :]                                   # (N,C_A)
        slope = (W_A.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)  # (N,K,K)
        logits = log_A_base.unsqueeze(0) + slope             # (N,K,K)
        log_A = log_softmax_logits(logits, dim=2)            # (N,K,K)

        score, idx = (delta.unsqueeze(2) + log_A).max(dim=1) # (N,K)
        psi[:, t] = idx
        delta = score + emis_log[:, t]

    # ---------------- backtracking ----------------
    paths = torch.empty(N, T, dtype=torch.long, device=device)
    last_state = delta.argmax(dim=1)
    paths[:, -1] = last_state
    for t in range(T - 1, 0, -1):
        last_state = psi[torch.arange(N, device=device), t, last_state]
        paths[:, t - 1] = last_state

    return paths.cpu()

Predicting Next-Year Donations

Obiettivo: Predire la distribuzione di donazioni del prossimo anno per un donatore e decodificare gli stati latenti passati usando un Hidden Markov Model (HMM) con emissioni Poisson dipendenti da covariate (GLM).

Input principali

birth_year, gender
Storico donazioni: history_years, history_counts
Covariate opzionali per emissioni (x_em_builder) e transizioni (x_A_builder)
Anni COVID per indicatore: covid_years

Predicting Next-Year Donations

Passaggi principali

Preparazione dati e covariate
- Normalizzazione di età e anno di nascita
- Costruzione delle covariate per stati iniziali (x_pi), transizioni (x_A) ed emissioni (x_em)
Emissioni Poisson
- Calcolo delle probabilità logaritmiche delle osservazioni dati gli stati (emis_log)
- Dimensione risultante: (N=1, T, K)
Inizializzazione stati latenti
- Logits iniziali log_pi0 combinando prior pi_base e covariate iniziali
- Normalizzazione con log_softmax → probabilità iniziali log_pi
Decodifica Viterbi
- Ricerca del percorso di stati più probabile (v_path)
- Backpointers psi per tracciare i percorsi ottimali
Forward Filtering
- Calcolo α_t (probabilità marginale di ogni stato al tempo t)
- Normalizzazione → distribuzione sugli stati all’ultimo anno osservato (alpha_T)
Predizione prossimo anno
- Transizione verso l’anno successivo usando A_next
- Emissione Poisson predittiva combinata con probabilità sugli stati
- Calcolo:
  - Probabilità di ciascuno stato p_next
  - Numero atteso di donazioni expected_next
  - Probabilità di almeno una donazione prob_donate_next
  - PMF fino a max_k con tail >= max_k+1

Predicting Next-Year Donations

Output

Sequenza stati passati: viterbi_states
Distribuzione di probabilità del prossimo anno: next_state_probs

Predizione numerica:

expected_next
prob_donate_next
pmf_next (dizionario 0..max_k + tail)

Years: [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023]
Counts: [0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0]
Viterbi states: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2]
Next year: 2024
Next-state probabilities: [0.371 0.06  0.569]
Expected next: 0.748
Prob donate next: 0.423
PMF next: {'0': 0.5772, '1': 0.2247, '2': 0.1194, '3': 0.0487, '4': 0.0184, '>=5': 0.0117}

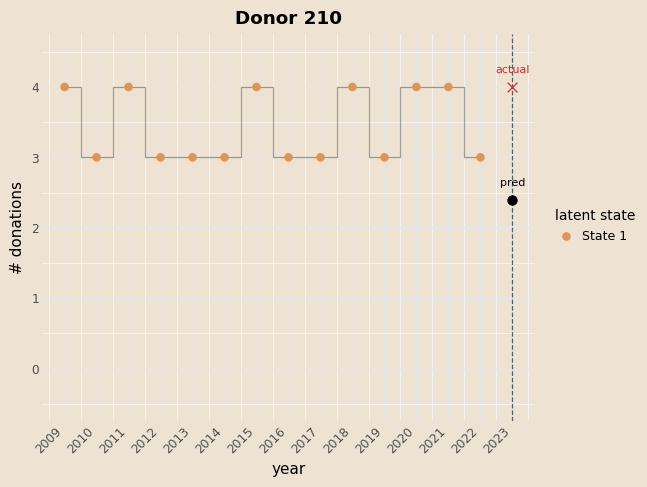
Prediction HMM-GLM

Obiettivo della funzione:

(‘y_pred_hmm’) → numero atteso di donazioni per ciascun individuo nell’anno successivo. \(\textbf{state\_prob}\) → distribuzione sugli stati latenti alla fine dell’anno osservato, usata per calcolare la predizione.
Inizializzazione della distribuzione sugli stati:

\[ \alpha^{(0)}_n = \text{softmax}\Big(\log \pi_{\text{base}} + x^{(n)}_{\pi} W_\pi^\top \Big), \quad n = 1,\dots,N \]

Propagazione in avanti per step futuri: \[ A^{(n)}_t = \text{softmax}_\text{row}\Big( \log A_{\text{base}} + W_A \cdot x^{(n)}_{A,t} \Big), \quad \alpha^{(t+1)}_n = \alpha^{(t)}_n \, A^{(n)}_t \]
Emissione Poisson (GLM per stato): \[ \eta^{(n)}_k = \beta_{k0} + \mathbf{x}^{(n)}_{\text{em},t} \cdot \beta_{k,1:}, \quad \lambda^{(n)}_k = \exp(\eta^{(n)}_k) \]
Predizione del conteggio atteso: \[ \mathbb{E}[y^{(n)}_{t+h}] = \sum_{k=1}^K \alpha^{(t+h)}_{n,k} \, \lambda^{(n)}_k \]
Risultato finale della funzione: \[ \text{y\_expected} = \big(\mathbb{E}[y^{(1)}_{t+h}], \dots, \mathbb{E}[y^{(N)}_{t+h}]\big), \quad \text{state\_dist} = \alpha^{(t+h)}_n \text{ per ogni individuo } n \]

GLM vs HMM-GLM

Metric	GLM	HMM	Abs diff	Rel diff %
pred mean	0.96	0.41	0.55	135.46%
obs mean	0.91	0.91	0.00	0.00%
MSE	1.0158	1.2934	-0.2777	-21.47%
Accuracy (round)	28.23%	40.73%	-12.50pp	-30.69%